정의 G=(V, E)
[ V = 공집합이 아닌 정점(vertex)들의 유한집합 ]
[ E = 정점들의 쌍인 간선(edge)들의 집합 ]
| 무방향 그래프 (Undirected Graph) |
방향 그래프 (Directed Graph) | |
 |
 |
 |
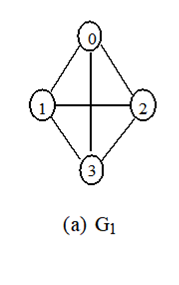
| V(G1) = {0, 1, 2, 3} E(G1) = {(0,1), (0,2), (0,3), (1,2), (1,3), 2,3)} |
V(G3) = {0, 1, 2} E(G3) = {<0,1>, <1,0>, <1,2>} <u,v> = <꼬리, 머리> |
|
E(G)의 간선 (u, v)에 대해
u와 v는 인접한다(adjacent)라고 하며
간선 (u, v)는 정점 u와 v에 부속된다(incident)고 한다.
완전 그래프 (Complete Graph)
n개의 정점을 갖는 무방향 그래프
간선 최대수 = n(n-1)/2
부분 그래프 (Sub Graph)
원래 그래프의 일부분. V(G') ⊆ V(G)
경로
E(G)에 속한 간선 (u, i1), (i1, i2), ... (ik, v)에 대해, 정점 u부터 정점 v까지의 경로는 u, i1, i2, ..., ik, v
경로의 길이
경로 상에 있는 간선들의 수
단순 경로 (Simple Path) : 처음과 마지막을 제외한 모든 정점들이 서로 다른 경로
단순 방향 경로 (Simple Directed Path) : 방향 그래프에서의 단순 경로
사이클 (Cycle) : 처음과 마지막이 같은 단순 경로
| 연결 그래프 (Connected Graph) | 비연결 그래프 |
| 무방향 그래프 G에서 임의의 두 정점 사이에 경로가 존재 하나의 연결요소로만 구성될 때 성립 |
|
 |
 |
| 연결 요소 (Connected Component) | 강력 연결 요소 (Strongly Connected Component) |
| 무방향 graph에서 최대 연결된 부분 그래프 | 방향 graph의 두 정점 u,v가 서로에 대한 방향 경로가 존재하여 이의 최대 강력 연결된 부분 그래프 |
 H1 = {0, 1, 2, 3}, H2 = {4, 5, 6, 7} |
 {0, 1}, {2} |
정점의 차수 (degree) : 정점에 부속한 간선들의 수
방향 그래프 - 진입 차수(indegree) & 진출 차수(outdegree)
∑di = 2e
[ e = 간선수 ] [ di = 정점 i의 차수 ]
그래프 표현법
1. 인접행렬 (Adjacency Matrix)
G = (V, E)에서 정점의 수가 n일 때, G의 인접행렬은 n×n의 2차원 배열
$n^2-n$개의 항 조사 (전체 - 대각선) → O($n^2$) 소요
밀집 graph에 주로 사용 (대부분 1)
무방향 그래프
$\sum_{j=0}^{n-1}A[i][j]$ = 정점 i의 차수
방향 그래프
$\sum_{j=0}^{n-1}A[i][j]$ = 정점 i의 진출 차수
2. 인접 리스트 (Adjacency List)
인접행렬의 n행들을 n개의 연결 리스트로 표현
무방향 그래프 - n개의 head node, 2e개의 list node → O(n+e) 소요
희소 graph에 주로 사용 (대부분 0)
| 그래프 | 인접 행렬 | 인접 리스트 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
가중치 그래프
간선에 가중치를 갖는 graph
표현 방법
① 인접 행렬
간선 O : 1 대신 가중치
간선 X : 0 혹은 ∞
② 인접 리스트
각 node에 weight field 추가
'자료구조' 카테고리의 다른 글
| 그래프 (Graph) - 최소비용 신장 트리 (Minimum Cost Spanning Tree) (0) | 2020.07.28 |
|---|---|
| 이진 탐색 트리 (Binary Search Tree, BST) (0) | 2020.07.25 |
| 최대 히프 (0) | 2020.07.25 |
| 트리 (Tree) (0) | 2020.07.24 |
| 자료구조 개념, 종류 (0) | 2020.07.12 |



